Quién más, quién menos, todo jugador de Scrabble® conoce algo llamado Elo. Es corriente oír a alguien decir “he subido/bajado Elo”, “he ganado a /perdido con uno con más/menos Elo que yo”,… Sabemos que es un método de clasificación, originalmente destinado al ajedrez, que hace que aumentemos o disminuyamos nuestra posición en él en función de quiénes son nuestros contrincantes en los torneos y de los resultados que obtengamos. Si jugamos todas las partidas de un torneo contra jugadores de nivel superior al nuestro, necesitaremos ganar pocas para que nuestro Elo suba. En cambio, si todos nuestros rivales tienen Elo inferior al nuestro, necesitaremos ganar muchas partidas para mantenernos y no bajar.
La base del sistema Elo es una fórmula que relaciona la probabilidad de victoria de un jugador, en función de la diferencia entre su Elo, y el de su rival. Imaginemos un hipotético jugador llamado A, que siempre tiene más Elo que sus contrincantes. En el siguiente gráfico, podemos ver la representación gráfica de las probabilidades de victoria del jugador A, en función de la diferencia de Elo con su rival. Obviamente, las probabilidades del otro jugador serán el resto hasta llegar al 100%.
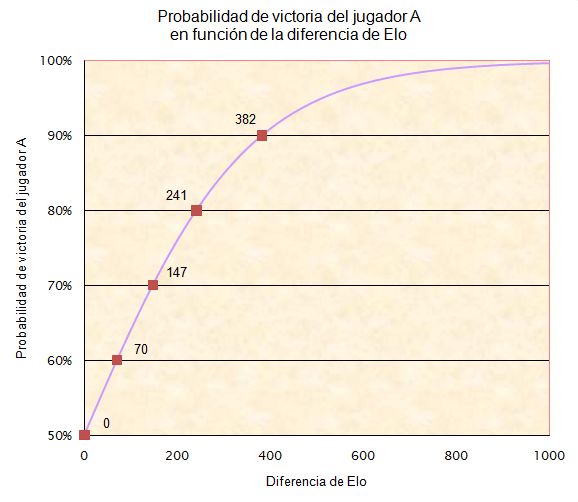 Los puntos marcados en el gráfico nos indican la diferencia de Elo entre los jugadores para que el Jugador A tenga unas probabilidades de victoria de 50, 60, 70, 80 y 90%.
Los puntos marcados en el gráfico nos indican la diferencia de Elo entre los jugadores para que el Jugador A tenga unas probabilidades de victoria de 50, 60, 70, 80 y 90%.
En numerosas ocasiones surge la duda de si el Elo es un sistema válido para clasificar a los jugadores de Scrabble® clásico. A veces se menciona que el factor suerte desvirtúa el escalafón, y que en numerosas ocasiones, los jugadores situados en la parte alta de la clasificación obtienen peores resultados de los que cabría esperar en función de su Elo.
Con la sana intención de esclarecer si el sistema de escalafón Elo, aplicado al Scrabble® Clásico no es más que una entelequia, o si realmente es un fiel reflejo del nivel de los jugadores, hemos llevado a cabo un estudio en el ámbito de la AJS, aprovechando la ingente cantidad de información obtenida tras la disputa de 15 torneos oficiales durante el año 2010.
Para ello, se han seleccionado, de cada torneo, aquellas partidas disputadas por dos jugadores que, con anterioridad al torneo, hayan jugado un mínimo de 50 partidas oficiales AJS. Esto supone un total de 908 partidas.
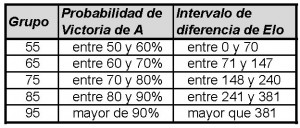
Estas partidas se han dividido en 5 grupos, con el siguiente criterio:
Siendo A, en todos los casos, el jugador con Elo superior.
Explicaremos un poco qué significan estos números.
Cuando se enfrentan dos jugadores con igual escalafón Elo, las probabilidades de que gane uno u otro son exactamente del 50%. Según la teoría, si disputaran 10 partidas del tirón, cada uno ganaría 5. Cuando la diferencia de Elo entre ambos es de 70, las probabilidades para el jugador A se sitúan en el 60%. Esto es, de 10 partidas, tendría que ganar 6.
El Grupo 55, entonces, lo encuadran las partidas en las que el jugador A tiene entre un 50 y un 60% de probabilidades de ganarla. De ahí, el valor 55, como intermedio entre ambos extremos. De forma equivalente se definen el resto de grupos.
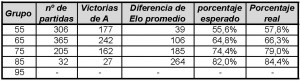
Una vez clasificadas las partidas por grupos, hemos realizado el cálculo de cuántas partidas, dentro de cada grupo, ha ganado el jugador A. Los resultados son los que se muestran a continuación:
Como se puede observar en estos resultados, las partidas disputadas en el ámbito de la AJS durante 2010 entre jugadores con escalafón consolidado son coherentes con la teoría del escalafón Elo. Incluso, se obtienen unos porcentajes reales ligeramente superiores a los teóricos, según la diferencia promedio de Elo entre los contrincantes, lo que indica que el Jugador A gana alguna partida más de las que el sistema prevé.
Por consiguiente, podemos afirmar que, a la luz del presente estudio, el escalafón Elo es un método adecuado y correcto para clasificar a los jugadores de Scrabble® Clásico.
Otras conclusiones que se pueden obtener son las siguientes:
– El efecto azar es un factor que está incluido dentro del escalafón, sin provocar distorsiones aparentes. Se puede inducir que la presencia del azar está presente en el escalafón mediante una menor dispersión de la clasificación. En el supuesto de un juego sin factor azar, la diferencia entre los valores máximo y mínimo de la clasificación sería superior a la existente.
– El presente estudio sanciona la bondad del sistema Elo aplicado al Scrabble® en el ámbito de la AJS de una forma global. Futuros trabajos en este ámbito, una vez el catálogo de partidas disponibles aumente hasta un número suficiente, podrán ir encaminados hacia:
- Aumento de los intervalos de diferencia de Elo
- Introducción en el estudio del escalafón Elo del jugador A, de modo que se permita confirmar si el sistema es independiente de esta variable o no.





Excelente análisis amigo! Ya me preguntaba que significaba esto per, Ud lo explica muy bien. Felicitaciones desde Venezuela !
Excelente estudio que da por tierra algunas teorías del tipo «igual, para mí el Elo está mal». La ciencia estadística debería servir para poner las cosas en su sitio. Felicitaciones Joan!